What makes mid-infrared
astronomy so demanding?
All infrared astronomy
is dependent to a greater or lesser degree on the atmosphere. It also depends
greatly on the amount of infrared radiation that comes from other sources
than the objects that we wish to study. Everything that is warm emits infrared
radiation: the sky, the telescope, its mirrors, etc.
The atmosphere and
its influence
Infrared astronomy is
carried out in a series of windows in the atmosphere that allow us to see
out into space. In between, the atmosphere is largely or totally opaque.
Infrared radiation is absorbed by various atmospheric components, in particular,
water vapour, carbon dioxide, ozone and methane. The very same gases that
make life on our planet possible by causing a natural greenhouse effect
block the radiation that we wish to detect from space. The amount of carbon
dioxide, ozone and methane are quite stable all over the Earth and from
night, but the water vapour is extremely variable, both from place to place
and from moment to moment.
CanariCam will be mounted
on the 10-m Gran Telescopio Canarias (GTC) in the Roque de los Muchachos
Observatory in La Palma (Canary Islands, Spain). This is a medium altitude
site (about 2300-m), but its latitude and the fact that the island of La
Palma is extremely steep (La Palma is a small island) means that it is
as dry or drier than many much higher observatories.
In the near infrared the
H and K windows (1.65 and 2.2 microns respectively) are broad and clean.
The J window is somewhat narrower and affected by water, but still easy
to use even from sea level. Other atmospheric windows though are neither
clean, nor stable.
CanariCam will work in
the 10 and 20-micron windows. If we look at the transmission of the atmosphere
over this wavelength range we see how important the atmosphere is. The
plots shown here are calculated for Mauna Kea when there is 1.2-mm of water
vapour above the observatory. In the Roque de los Muchachos Observatory
around 10-15% of the time the water vapour
over the observatory is as good as this or better, corresponding to what
is meteorologically an extremely dry atmosphere - at sea level the amount
of water vapour even on a cloudless day is usually some 30 to 50-mm (this
means that if all the water were suddenly to rain out it would cover the
ground with a layer of water this deep).
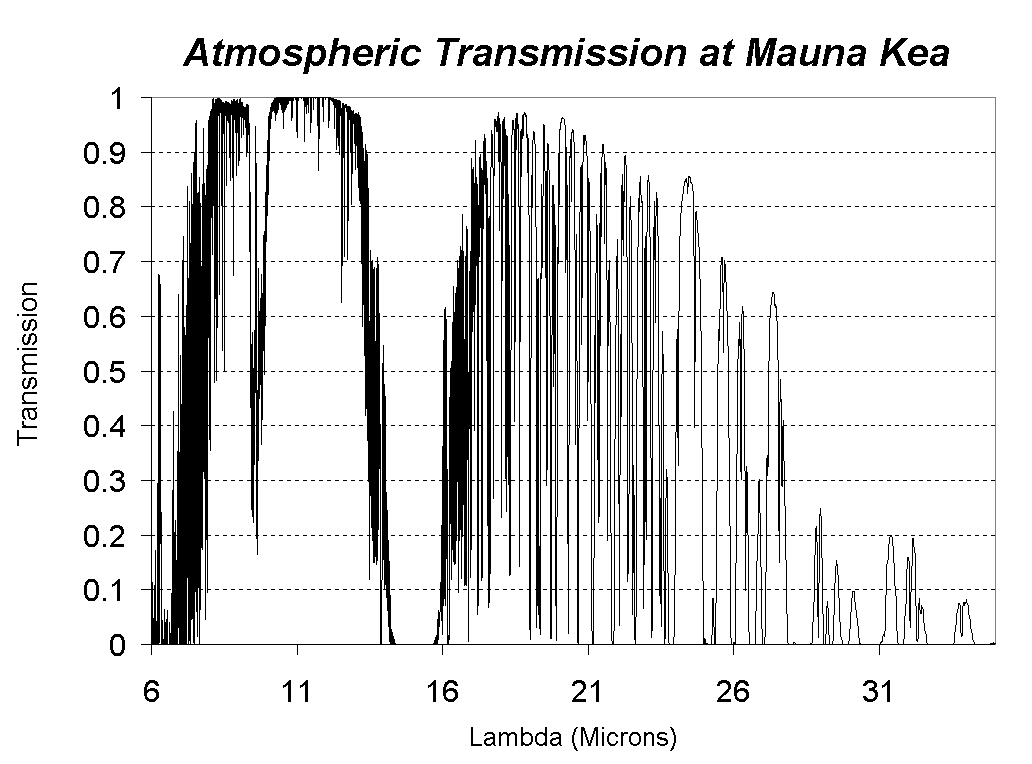
The theoretical atmospheric
transmission at Mauna Kea. This plot was generated using data produced
using the program IRTRAN4, obtained from the UKIRT worldwide web page here.
The calculations were carried out for a 1.2-mm column of precipitable water
vapour and a resolution of 3000.
Around 11 microns there
is a region where the atmosphere is almost completely transparent and a
narrower one at 8 microns - in between atmospheric ozone makes this window
almost totally opaque. Around 15 microns Carbon dioxide completely blocks
out infrared radiation from space. We see that the window at 20 microns
has some good, very transparent regions, but these are narrow and separated
by deep chasms of absorption by water vapour.
In the following plots
we can see these regions in detail. CanariCam will work from about 7.5
microns to about 24 microns (these limits depend on the atmosphere at the
short wavelength end and on the detector at the long wavelength limit).
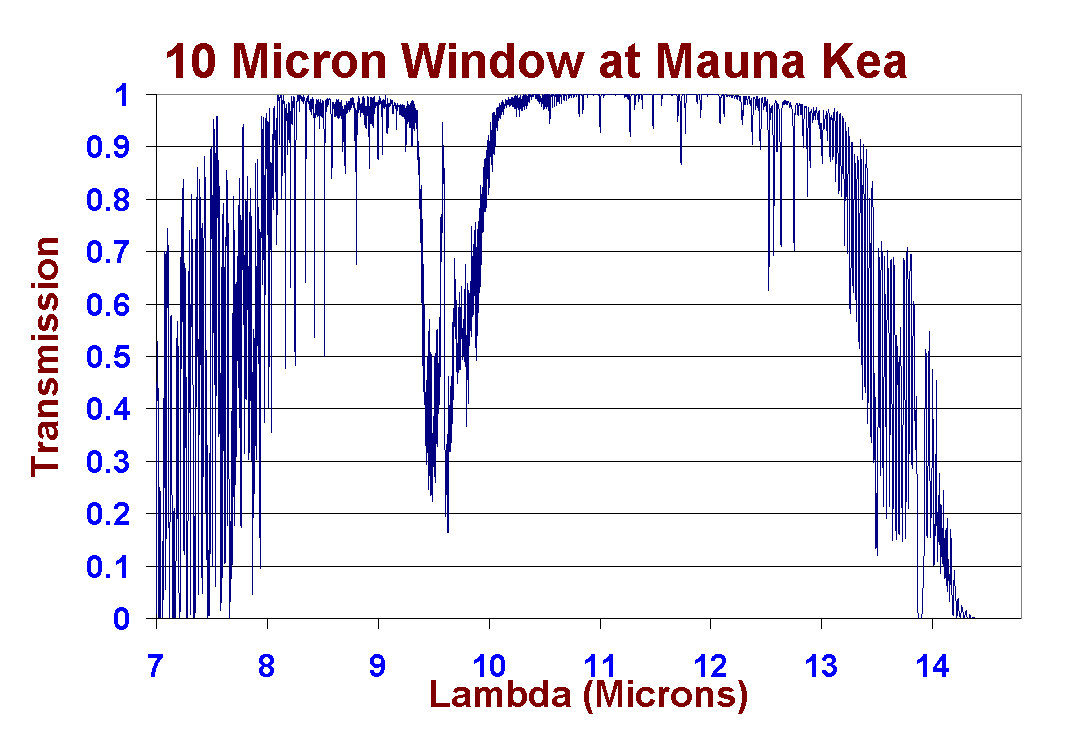
The theoretical atmospheric
transmission in the 10 micron window at Mauna Kea on an expanded scale.
This plot was generated using data produced using the program IRTRAN4,
obtained from the UKIRT worldwide web page here.
The calculations were carried out for a 1.2-mm column of precipitable water
vapour and a resolution of 3000.
As it is quite transparent
in its best regions the 10-micron window has been quite widely used in
the past from the Earth's surface.
CanariCam will use a broad
filter to exploit this transparency, plus a series of narrow filters in
this window to look at individual lines and emissions from astronomical
objects.
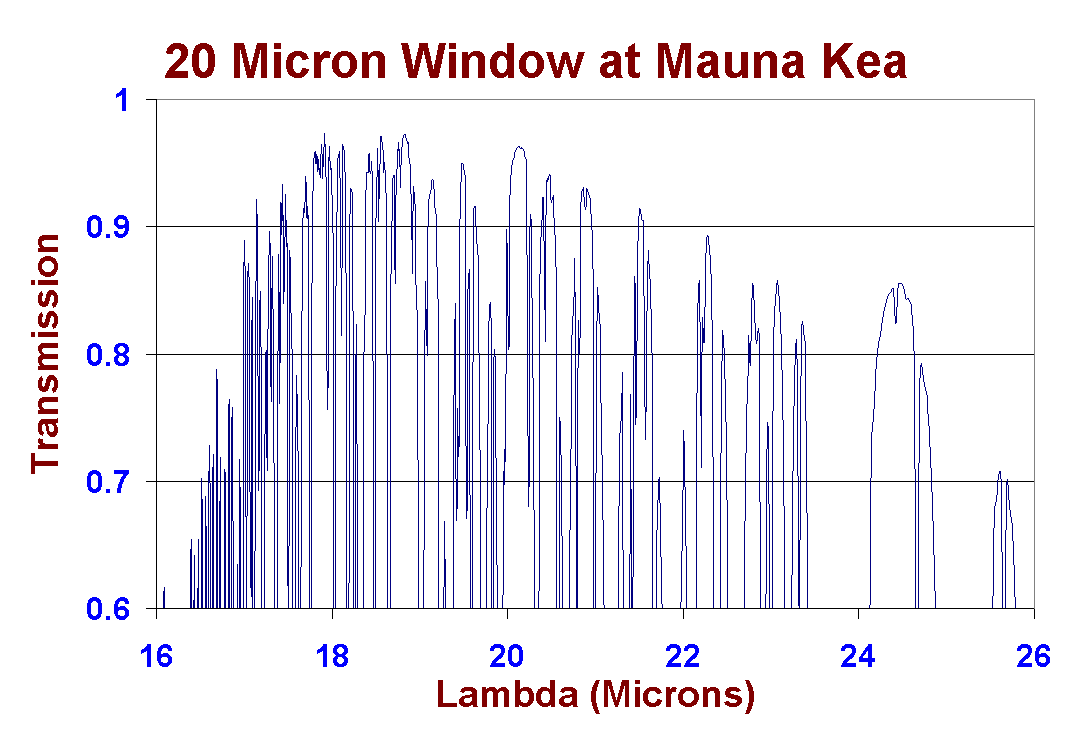
The theoretical atmospheric
transmission in the 20 micron window at Mauna Kea on an expanded scale.
This plot was generated using data produced using the program IRTRAN4,
obtained from the UKIRT worldwide web page here.
The calculations were carried out for a 1.2-mm column of precipitable water
vapour and a resolution of 3000.
Deep water vapour lines
cross the 20-micron window. In some regions there is still 95% transmission
by the atmosphere, but these are narrow and separated by highly opaque
areas. CanariCam will use both a broad filter that covers the entire window,
and a series of very narrow filters that take in the best of the individual
regions of this window.
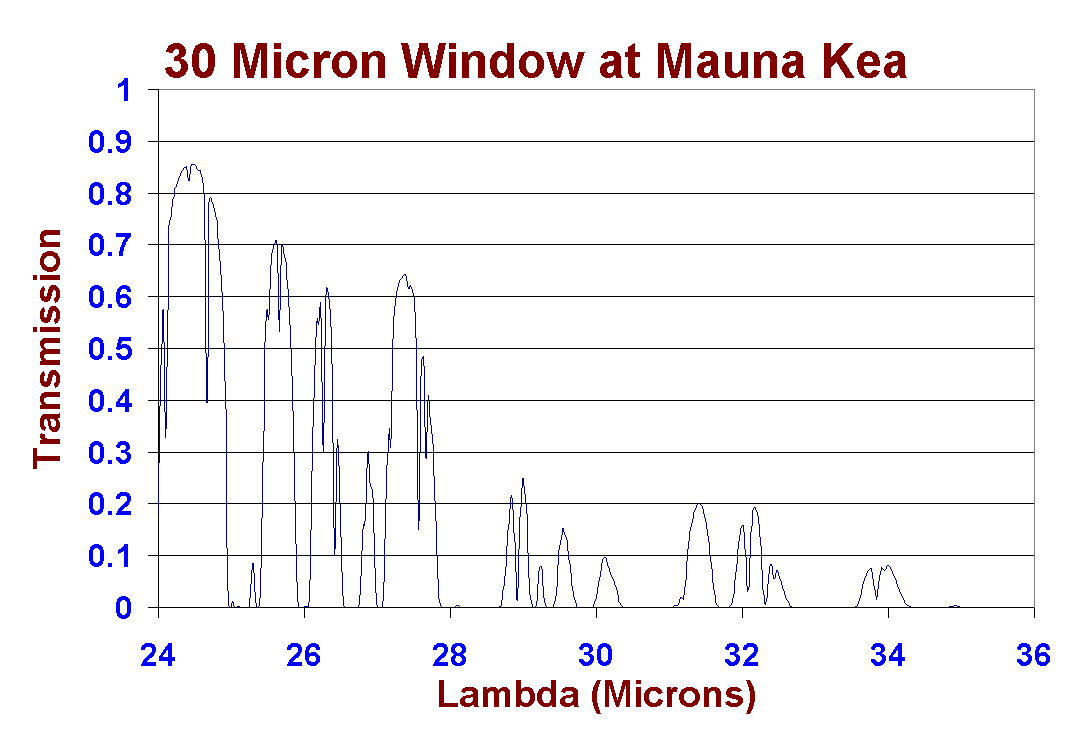
The theoretical atmospheric
transmission in the 30 micron window at Mauna Kea on an expanded scale.
This plot was generated using data produced using the program IRTRAN4,
obtained from the UKIRT worldwide web page here.
The calculations were carried out for a 1.2-mm column of precipitable water
vapour and a resolution of 3000.
Here we see why beyond
24-microns science returns are not guaranteed. The atmospheric transparency
drops off rapidly and the windows become ever fewer and more opaque. As
the sensitivity of the detector will probably drop off sharply from 24
microns, we can see that this region of the spectrum is a very poor one
for ground-based science. CanariCam will have a narrow filter at 24.5 microns
to exploit the best of these windows that, in very dry conditions could
give extremely important results. This filter will allow astronomers to
examine cool objects in space, possibly even Kuiper Belt comets that cannot
be detected at shorter wavelengths and planets orbiting around other stars
at about the distance of Uranus or Neptune.
Click here
to see more about atmospheric conditions at the GTC site.
The influence of the
warm background
Mid-infrared astronomy
is greatly influenced by the fact that everything emits infrared radiation
due to the very fact of it being warm. An object at room temperature emits
radiation best and in largest quantity around 10 microns. Cooler objects
emit at longer wavelengths.
What this means in practice
is that the part of the light that the mirror of the telescope does not
reflect is reemited as heat and detected by CanariCam and the parts of
the telescope structure that the mirror sees also emit infrared radiation.
In the same way, the part of the light that the atmosphere absorbs is also
reemited as heat and detected by the instrument.
In other words, any star
or galaxy that we wish to measure is bathed in a haze of radiation from
the instrument's surroundings. Often the galaxy is many millions of times
fainter than this background radiation.
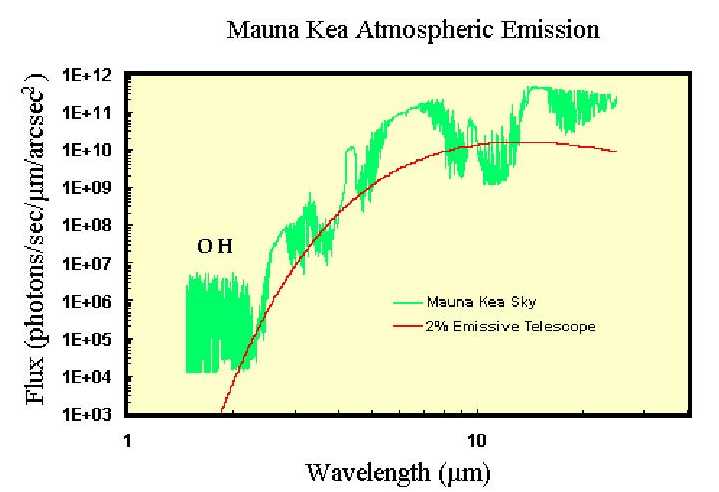
Mauna Kea atmospheric
transmission compared to the emissivity of a 2% emissive telescope for
2-mm of water vapour. Note how a mid-IR instrument is limited by the telescope
emisivity over a significant part of the 10 micron window. Image: University
of Florida Astronomy Group.
Here we see the relative
contributions of background light from the sky (green line) and a perfect
telescope (red line). Here we assume that there is 2-mm of water vapour
and that the telescope reflects 98% of the light that reaches its mirror
(an optical telescope may not pass 80% unless it has recently been cleaned
and 95% is very difficult to attain). By making the optics as clean and
reflective as possible (this includes both the telescope mirrors and the
mirrors inside CanariCam) we can make the radiation from the atmosphere
the deciding factor in many cases, but in the best parts of the 10-micron
window what limits us is the optical path.
The contribution to the
background from the telescope is minimised by making the telescope structure
as light as possible (in that way we "see" the minimum of support structure)
and by taking careful measures to maintain the mirrors very clean. This
includes removing segments from the GTC mirror every week to clean them
on a cyclical basis so that every six months approximately the entire mirror
surface has been renewed. Giving the telescope a gold-coated secondary
mirror may make another improvement in the future, as gold reflects infrared
light very efficiently - much more so than aluminium or silver. These factors
are beyond the control of CanariCam.
The CanariCam team can
control what happens inside the instrument. Gold mirrors, each 99% reflective
for infrared light are used. The detector and mirrors are cooled to below
30K (-245ºC approximately) and a special shield (a light baffle) cooled
to the same temperature blocks out all light that does not come from the
telescope mirror.
We can also improve the
instrument's sensitivity significantly by observing in cold and very dry
conditions that will reduce the background still further. By scheduling
the most critical observations in queue observing mode we can take advantage
of the very best conditions in the observatory, whenever they happen.
How does CanariCam
detect stars one million times fainter than the sky?
We use a special technique
to detect faint sources. We do not "stare" at a fixed point (our star)
but rather flip between different positions to compare the signals received.
Two movements are involved: a fast chopping movement and a slow nod.
If we are observing a
point source (a star), we chop between two positions on the sky separated
by about 10 arcseconds 5 times each second. Making the GTC's secondary
mirror oscillate quickly in a very precisely controlled manner does this.
Our star, which is probably completely invisible, changes between two positions
(termed "on" and "off") on the detector. We subtract one exposure from
the other and remove the sky background and most of the noise in the image
and are left with a positive and a negative image of our star. However,
there may be gradients and slow variations of the sky across the field
of view so, to eliminate these, once or twice a minute we move the telescope
to a new position (termed a "nod") and integrate again in exactly the same
way as before.
We end up with two positive
and two negative images of the star as in the OSCIR data shown below.
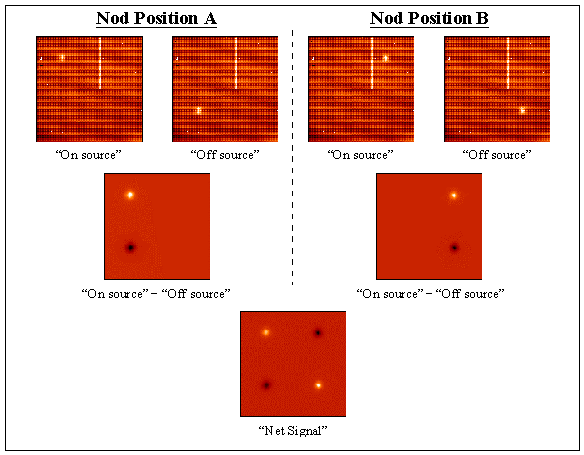
Real OSCIR data showing
the sky subtraction method used in the mid-IR to detect faint objects.
In this case the object being observed is a bright star that can be seen
in the original frames. Image: University of Florida Astronomy Group.
These are then combined
to give the final summed image.
This is a very simple
case. We can even see the star in the unprocessed images (which will rarely
be the case on the telescope with real sources). How though do we manage
to detect a star that has 2000 counts above a sky that may have one million?
The answer is quite simple.
Although the sky has one million counts, the noise in the sky background
- the random fluctuations from pixel to pixel, or Poisson noise - is the
square root of this... 1000 counts. In other words, we have twice as much
signal from the star as noise from the sky and our object is easy to detect
by the process above.
What about much fainter
objects? As we integrate for longer, the noise in the sky goes up as the
square root of the total exposure time, but the signal from the star increases
with the exposure time. In other words, every time we multiply the exposure
time by a factor of 4 we get twice as much signal to noise and detect objects
0.8 magnitudes fainter.
One big advantage of CanariCam
is its small pixels and exceptional image quality. The image of a source
is effectively limited to a diameter of two pixels and because the pixels
are small, the sky background in each pixel is minimised. This maximises
the sensitivity.
CanariCam should be able
to detect magnitude 11.5 at 10 microns in a 100s exposure with a signal
to noise ratio of 5 (this is much better than IRAS and a little better
than ISO and some 4-5 magnitudes better than even the 4-m telescope at
CTIO) and has the huge advantage that it can make very long, deep exposures.
In ten thousand seconds (a fairly standard deep exposure for astronomers),
CanariCam will give a good detection at magnitude 14 at 10 microns.
Here is a case of real
OSCIR data of a source (the central region of the Starburst galaxy NGC
253) that is both invisible in the raw frames and extended so that the
chop must reach out to blank sky to one side of the source, outside the
field of view.
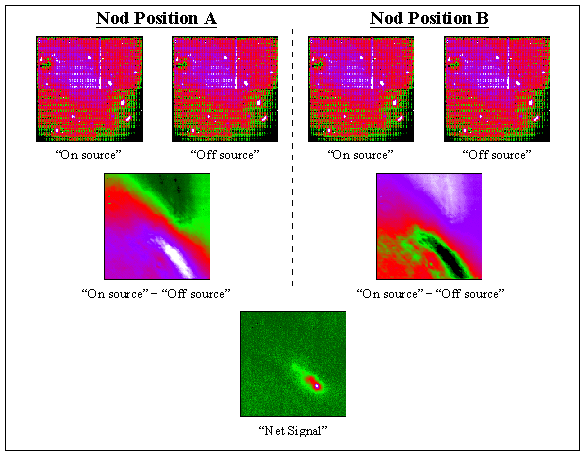
Real OSCIR data showing
the sky subtraction method used in the mid-IR to detect faint objects.
This is the case of a faint extended object (a Starburst galaxy) that cannot
be seen in the original data. Image: University of Florida Astronomy Group.
The top row of four images
shows the raw data frames from the two secondary mirror positions at each
of the two nod positions (called "Nod Position A" and "Nod Position B")
of the telescope. Fixed-pattern offsets due to pixel-to-pixel variations
and offsets between the 16 channels of the acquisition electronics dominate
these images. The background counts in these raw images correspond to 7.4x
108 e-/s. Each raw image consists of ~5 minutes of
total integration time (i.e. 15,000 frames co-added using a 20 ms frame
integration time and the N-band filter) obtained in the chop/nod sequence
as described above.
The second row of two
images shows the "chop-differenced" data derived from the subtraction of
the on-source and off-source data in the two nod positions of the telescope.
Note that the dominant pattern (principally a gradient along the diagonal
connecting the lower-left to upper-right corners of the images) has changed
sign between the two chop-differenced frames. However, since the subtraction
is always done as "on-source minus off-source", the source signal remains
positive in both chop-differenced frames. The signal levels in these differenced
frames range ±3.2x106 e-/s, which is ~0.4%
of the raw background signal. Finally, the bottom row shows the net signal
obtained by adding together the two chop-differenced frames shown in the
middle row. No other processing has been done to the data other than the
additions and subtractions as described above.
The net signal is the
result of a total exposure of ~20 minutes in which half that time is actually
spent imaging the off-source "reference" position. The signal level at
the "tail" of this source near the middle of the frame is ~6.4´ 104
e-/s. This is about four orders of magnitude below the background level
shown in the raw frame. In fact, the signal-to-noise ratio at this level
in each pixel is about seven, so that the effective background subtraction
is more nearly five orders of magnitude below the background!
 Back to the Main CanariCam Page.
Back to the Main CanariCam Page.
Latest update: February
19th 2002
Pages maintained by: Mark Kidger






