LAW II: THE AREA LAW
(1609 and 1621)
1. Modern form
A planet moves in its elliptic orbit so that the line joining the
planet to the Sun sweeps out equal areas in equal intervals of time.
2. Kepler stated his
result in Astronomia nova (1609), in
Chapter 60 (KGW III p.377 lines 3-5; Donahue p.593): 'the time [taken by Mars as
it moves in its orbit] is measured by the area'.
3. What Kepler initially discovered
The figure below shows the planet at a position P on its path CFD
whose (major) diameter is CD, circumscribed by the circle diameter CD centre B. Q is a typical point of that circle,
determined by the angle ÐQBC = b at the
centre, with QPH the ordinate linking the associated points Q and P. A is the position of the Sun, and we follow
Kepler by describing the point A as 'the eccentric point' (because it is
'off-centre'). Then for consistency with
Law I, we shall express AB, the eccentric distance, as a proportion 
of the radius 
of the circle. (For the separation of the circle and the
ellipse to be visible, the eccentric distance always has to be greatly
exaggerated.)
Kepler established that when the planet is at position P in its
elliptic orbit, the time taken is represented by the area of the corresponding sector:
in the figure, the time taken to reach P (from starting-point C) is proportional
to area PAC of the ellipse swept out.
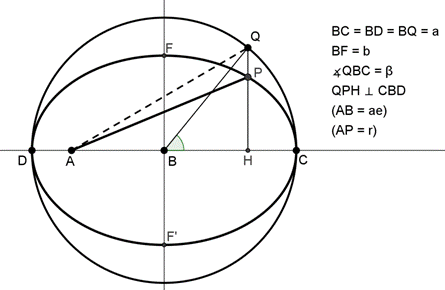
Figure: The Area Law
The ellipse is defined mathematically by the
ratio-property of the ordinates, which Archimedes had stated in his work On Conoids and Spheroids, Prop.4:
In Astronomia nova Chapter
59 Kepler proved geometrically that the area of the ellipse sector PAC determined
by the position of the point P can be exactly found, because it is proportional
to the associated area QAC of the circle.
And this gave a value for the time that matched the distance at P,
closely in accordance with Tycho Brahe's extremely accurate naked-eye
observations.
4. Kepler's proof of
that discovery
In the proposition from On Conoids and Spheroids already mentioned, Archimedes had proved
that:
Kepler adapted this result to good effect in Chapter 59
Protheorema III. He derived (KGW III
p.368 lines 3-4):
Then Kepler applied Euclid's Elements VI, 1
(since the two triangles have the same base), to state (KGW III p.368 lines
6-7) that:
Thence, as Kepler said 'by composition' of (3) and (4) – that is,
by combining the two pairs of pieces using his diagram above – he derived (KGW
III p.368 lines 7-8):
This completes Kepler's proof that the area of the ellipse sector
which defines the position of the point P can be exactly determined by the associated
area of the circle.
(And we add that Kepler had shown much earlier, in Chapter 40 (KGW
III p.265 lines 8-10), that area QAC can be split into pieces in the following
way:
so that the area of sector QAC evidently depends on the angle at
the centre of the circle, and can thus be easily evaluated.) Hence the area of the ellipse sector
completed by the planet can be expressed in terms of known quantities, and is
accordingly itself regarded as known.
We shall now present these expressions of the time taken to reach
P in symbolic notation for the benefit of modern readers (writing 
):
or,
Hence, the variation in time is measured in terms of the angle b at the centre:
This expression is often referred to nowadays as 'Kepler's Equation'
– he discussed it, with numerical examples, at the end of Chapter 60. But, it is more accurately described as
'Kepler's formula for time in orbit'.
5. The final
achievement
However, that is only the first strand of the demonstration. Sharp-eyed readers will have spotted that,
while the measure of area has been soundly established, there is no matching
theory of time (some initial assumption about how equal amounts of time should
be represented geometrically in the diagram).
In ancient astronomy time was always represented by an angle, so when
Kepler came to deal with this second strand in his mature work of 1621: Epitome Book V, Part I, Section 4 (KGW
VII) he defined equal small (increment-sized) quantities of time by equal small
angles taken at the centre B of the circle.
These angles determined equal small circular sectors (increments of
area) that Kepler then (using only the geometry of Euclid) manipulated
mathematically into equivalence with equal small elliptic sectors round the Sun
at A[*]. So eventually Kepler achieved an incremental
(near-infinitesimal) proof of the Area law (this mature version is illustrated
on numerous websites).
Therefore Kepler's formulation constituted a valid proof that time
in orbit was represented by area – but only in an elliptic orbit, when the Sun
was the focus and the centre of motion.
[The Area-Time proposition in all generality was of course demonstrated
by Newton, not until 1687.]
For more details of Kepler's method, see:
A E L Davis
ael.davis@imperial.ac.uk