Representación gráfica de funciones y datos

Exite una gran variedad de módulos para hacer gráficos de todo tipo con Python, pero el estándar de facto en ciencia es matplotlib. Se trata de un paquete grande y relativamente complejo que entre otros contiene dos módulos principales, pyplot y pylab.

pyplot ofrece una interfaz fácil para crear gráficos fácilmente, automatizando la creación de figuras y ejes automáticamente cuando hace un gráfico. Por otra parte, pylab combina la funcionalida de pyplot para hacer gráficos con funcionalidad de numpy para hacer cálculos con arrays usando un único espacio de nombres muy parecido a Matlab.

Por esto, es posible que en la literatura nos encontremos dos formas comunes de usar la interfaz de matplotlib:

# importar todas las funciones de pylab
from pylab import *

# importar el módulo pyplot
import matplotlib.pyplot as plt

Al usar la primera opción también importamos numpy como np, entre otras cosas. En general, se recomienda usar pylab cuando se trabaja interactivamente y pyplot cuando se usan programas ejecutables.

Empecemos creando el gráfico más sencillo posible:

In [1]: from pylab import *      # importar todas las funciones de pylab
In [2]: x = arange(10.)          # array de floats, de 0.0 a 9.0

In [3]: plot(x)                  # generar el gráfico de la función y=x
Out[3]: [<matplotlib.lines.Line2D object at 0x9d0f58c>]

In [4]: show()                   # mostrar el gráfico en pantalla

Hemos creado un gráfico que representa diez puntos en un array y luego lo hemos mostrado con show(); esto es así porque normalmente solemos hacer varios cambios en la gráfica, mostrándolos todos juntos. Sin embargo, cuando trabajamos interactivamente, por ejemplo con la consola ipython podemos activar el modo interactivo para que cada cambio que se haga en la gráfica se muestre en el momento, mediante la función ion(), de esta manera no hace falta poner show() para mostrar la gráfica cada vez que se haga plot():

In [1]: ion()             # Activo el modo interactivo
In [2]: plot(x)           # Hago un plot que se muestra sin hacer show()
Out[2]: [<matplotlib.lines.Line2D object at 0x9ffde8c>]

Recordar que este modo interactivo sólo está disponible en la consola avanzada ipython pero no lo está en la consola estándar de Python. Otra posibilidad es usar el comando mágico %pylab de ipython, de esta manera se carga automáticamente pylab, se activa el modo interactivo y además se importa el módulo numpy y todas sus funciones; al hacerlo, se hace lo siguiente:

import numpy
import matplotlib
from matplotlib import pylab, mlab, pyplot
np = numpy
plt = pyplot

from IPython.display import display
from IPython.core.pylabtools import figsize, getfigs

from pylab import *
from numpy import *

Fíjense cómo el comando plot() que hemos usado hasta ahora devuelve una lista de instancias de cada dibujo. Una instancia es una referencia a un elemento que creamos, en este caso la línea en gráfica. En este caso es una lista con un sólo elemento, una instancia Line2D. Podemos guardar esta instancia para referirnos a este dibujo (a la línea en concreto) más adelante haciendo:

In [3]: mi_dibujo, = plot(x)

Ahora la variable mi_dibujo es una instancia o «referencia» a la línea del dibujo, que podremos manipular posteriormente con métodos que se aplican a esa instancia dibujo. Nótese que después de mi_dibujo hay una coma; esto es para indicar que mi_dibujo debe tomar el valor del primer (y en este caso el único) elemento de la lista y no la lista en sí, que es lo que habría ocurrido de haber hecho mi_dibujo = plot(x) (erróneamente). Esto es habitual al trabajar con listas, veámoslo con un ejemplo:

a = [3, 5]
# Así ``a`` es una lista, que contiene dos valores

a, b = [3, 5]
# Así desempaquetamos los elementos de la lista y a=3 y b=5
# Esto funciona porque pusimos tantas variables como elementos en la lista

Pero si la lista sólo tiene un elemento ¿cómo desempaquetamos ese elemento?. Veamos:

a = [3]  # Así, ``a`` es una lista y no el número 3

a, = [3] # Si añadimos una coma indicamos que queremos meter ese único
         # elemento en una variable, en lugar de usar la lista

Y esto es justo lo que hicimos con mi_dibujo, = plot(x), para hacer que mi_dibujo contenga una instancia y no una lista de instancias, que es lo que devuelve plot().

La sintaxis básica de plot() es simplemente plot(x, y), pero si no se incluye la lista x, ésta se reemplaza por el número de elementos o índice de la lista y, por lo que es equivalente a hacer plot(range(len(y)), y). En la gráfica del ejemplo anterior no se ven diez puntos, sino una línea contínua uniendo esos puntos, que es como se dibuja por defecto. Si queremos pintar los puntos debemos hacerlo con un parámetro adicional, por ejemplo:

In [4]: plot(x, 'o') # pinta 10 puntos como o
Out[4]: [<matplotlib.lines.Line2D object at 0x8dd3cec>]

In [5]: plot(x, 'o-')        # igual que antes pero ahora los une con una linea continua
Out[5]: [<matplotlib.lines.Line2D object at 0x8dd9e0c>]

En este caso el “o” se usa para dibujar puntos gruesos y si se añade “-“ también dibuja la línea contínua. En realidad, lo que ha sucedido es que se dibujaron dos gráficos uno encima del otro; si queremos que se cree un nuevo gráfico cada vez que hacemos plot(), debemos añadir el parámetro hold=False a plot():

mi_dibujo, = plot(x*2, 'o', hold=False)

El tercer parámetro de la función plot() (o segundo, si no se incluye la variable x) se usa para indicar el símbolo y el color del marcador. Admite distintas letras que representan de manera única el color, el símbolo o la línea que une los puntos; por ejemplo, si hacemos plot(x, 'bx-') pintará los puntos con marcas «x», de color azul («b») y los unirá además con líneas contínuas del mismo color. A continuación se indican otras opciones posibles:

Colores

Símbolo	Color
“b”	Azul
“g”	Verde
“r”	Rojo
“c”	Cian
“m”	Magenta
“y”	Amarillo
“k”	Negro
“w”	Blanco

Marcas y líneas

Símbolo	Descripción
“-“	Línea continua
“–”	Línea a trazos
“-.”	Línea a puntos y rayas
“:”	Línea punteada
“.”	Símbolo punto
“,”	Símbolo pixel
“o”	Símbolo círculo relleno
“v”	Símbolo triángulo hacia abajo
“^”	Símbolo triángulo hacia arriba
“<”	Símbolo triángulo hacia la izquierda
“>”	Símbolo triángulo hacia la derecha
“s”	Símbolo cuadrado
“p”	Símbolo pentágono
“*”	Símbolo estrella
“+”	Símbolo cruz
“x”	Símbolo X
“D”	Símbolo diamante
“d”	Símbolo diamante delgado

Para borrar toda la figura se puede usar la función clf(), mientras que cla() sólo borra lo que hay dibujado dentro de los ejes y no los ejes en si.

Se pueden representar varias parejas de datos con sus respectivos símbolos en una misma figura, aunque para ello siempre es obligatorio incluir el valor del eje x:

In [8]: clf()   # Limpiamos toda la figura

In [9]: x2 = x**2   # definimos el array x2

In [10]: x3 = x**3    # definimos el array x3

In [11]: # dibujamos tres curvas en el mismo gráfico y figura
In [12]: plot(x, x, 'b.', x, x2, 'rd', x, x3, 'g^')
Out[13]:
[<matplotlib.lines.Line2D object at 0x8e959cc>,
<matplotlib.lines.Line2D object at 0x8eb75cc>,
<matplotlib.lines.Line2D object at 0x8eb788c>]

Esta lista de salida de plot() contiene 3 instancias que se refieren a 3 elementos diferentes de la gráfica.

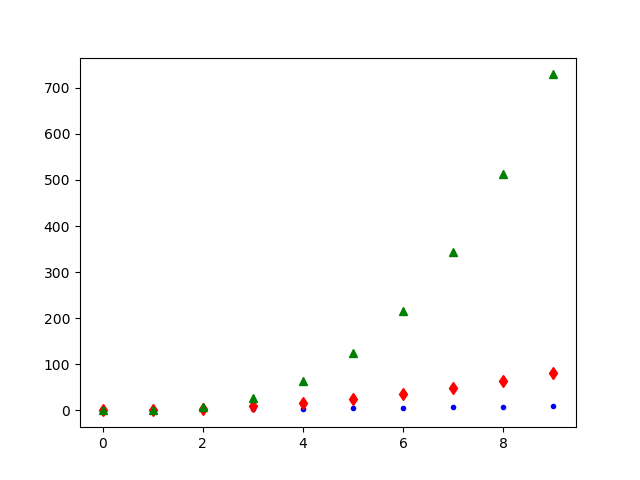
Es posible cambiar el intervalo mostrado en los ejes con xlim() e ylim() :

In [20]: xlim(-1, 11)     # nuevos límites para el eje OX
Out[20]: (-1, 11)

In [21]: ylim(-50, 850)   # nuevos límites para el eje OY
Out[21]: (-50, 850)

Además del marcador y el color indicado de la manera anterior, se pueden cambiar muchas otras propiedades de la gráfica como parámetros de plot() independientes como los de la tabla adjunta:

Parámetro	Significado y valores
alpha	grado de transparencia, float (0.0=transparente a 1.0=opaco)
color o c	Color de matplotlib
label	Etiqueta con cadena de texto, string
markeredgecolor o mec	Color del borde del símbolo
markeredgewidth o mew	Ancho del borde del símbolo, float (en número de puntos)
markerfacecolor o mfc	Color del símbolo
markersize o ms	Tamaño del símbolo, float (en número de puntos)
linestyle o ls	Tipo de línea, “-“ “–” “-.” “:” “None”
linewidth o lw	Ancho de la línea, float (en número de puntos)
marker	Tipo de símbolo,”+” “*” “,” “.” “1” “2” “3” “4” “<” “>” “D” “H” “^” “_” “d” “h” “o” “p” “s” “v” “x” “|” TICKUP TICKDOWN TICKLEFT TICKRIGHT

Un ejemplo usando más opciones sería este:

In [26]: plot(x, lw=5, c='y', marker='o', ms=10, mfc='red')
Out[26]: [<matplotlib.lines.Line2D object at 0x8f0d14c>]

También es posible cambiar las propiedades de la gráfica una vez creada, para ello debemos capturar las instancias de cada dibujo en una variable y cambiar sus parámetros. En este caso a menudo hay que usar draw() para actualizar el gráfico,

# Hago tres dibujos, capturando sus instancias
# en las variables p1, p2 y p3
In [26]: p1, p2, p3 = plot(x, x,'b.',x, x2, 'rd', x, x3, 'g^')

In [27]: show()                 # Muestro en dibujo por pantalla
In [28]: p1.set_marker('o')     # Cambio el símbolo de la gráfica 1
In [29]: p3.set_color('y')      # Cambio el color de la gráfica 3
In [30]: draw()                 # Hacer los cambios

usando instancias similares poder cambiar prácticamente todas las propiedades de nuestro gráfico sin tener que rehacerlo. Por tanto es buena costumbre guardar las instancias en variables cuando trabajemos interactivamente.

Trabajando con texto dentro del gráfico

Exiten funciones para añadir texto (etiquetas) a los ejes de la gráfica y a la gráfica en sí; éstos son los más importantes:

In [50]: x = arange(0, 5, 0.05)

In [51]: p, = plot(x,log10(x)*sin(x**2))

In [52]: xlabel('Eje X')        # Etiqueta del eje OX
Out[52]: <matplotlib.text.Text object at 0x99112cc>

In [53]: ylabel('Eje Y')        # Etiqueta del eje OY
Out[53]: <matplotlib.text.Text object at 0x99303cc>

In [54]: title('Mi grafica')    # Título del gráfico
Out[54]: <matplotlib.text.Text object at 0x993802c>

In [55]: text(1, -0.4, 'Nota')  # Texto en coodenadas (1, -0.4)

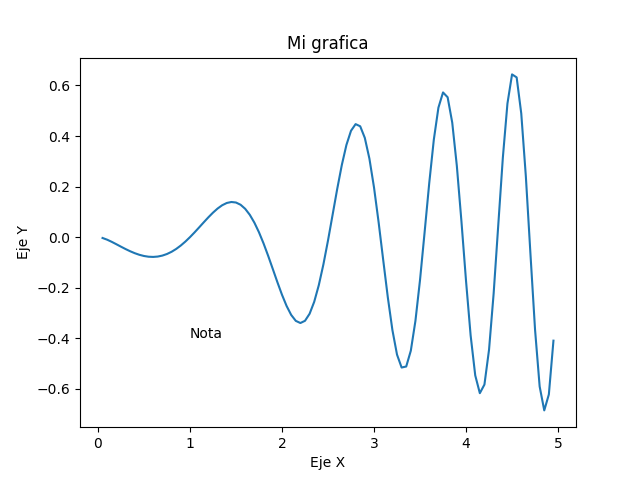
En este ejemplo, se usó la función text() para añadir un texto arbitrario en la gráfica, cuya posición se debe dar en las unidades de la gráfica. Cuando se utilizan textos también es posible usar fórmulas con formato LaTeX. Veamos un ejemplo:

from math import *
from numpy import *

t = arange(0.1, 20, 0.1)

y1 = sin(t)/t
y2 = sin(t)*exp(-t)
p1, p2 = plot(t, y1, t, y2)

# Texto en la gráfica en coordenadas (x,y)
texto1 = text(2, 0.6, r'$\frac{\sin(x)}{x}$', fontsize=20)
texto2 = text(13, 0.2, r'$\sin(x) \cdot e^{-x}$', fontsize=16)

# Añado una malla al gráfico
grid()

title('Representacion de dos funciones')
xlabel('Tiempo / s')
ylabel('Amplitud / cm')

show()

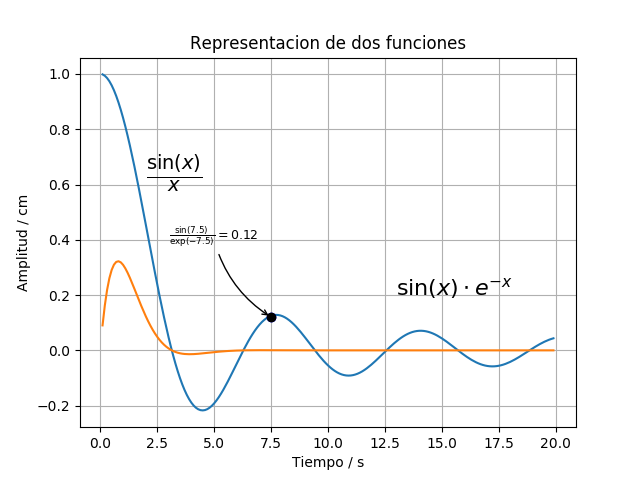
Aquí hemos usado código LaTeX para escribir fórmulas matemáticas, para lo que siempre hay que escribir entre r'$ formula $' y usado un tamaño de letra mayor con el parámetro fontsize. En la última línea hemos añadido una malla con la función grid().

También podemos hacer anotaciones de partes de la gráfica usando flechas, para lo que hay que indicar las coordenadas del punto a señalar, a donde apuntará la flecha y las coordenadas de texto asociado:

# Punto a señalar en la primera gráfica
px = 7.5
py = sin(py)/py

# Pinto las coordenadas con un punto negro
punto = plot([px], [py], 'bo')

# Hago un señalización con flecha
nota = plt.annotate(r'$\frac{\sin(7.5)}{\exp(-7.5)} = 0.12$',
         xy=(px, py),
         xycoords='data',
         xytext=(3, 0.4),
         fontsize=9,
         arrowprops=dict(arrowstyle="->",
         connectionstyle="arc3,rad=.2"))

Nota

LaTeX es un sistema de escritura orientado a contenidos matemáticos muy popular en ciencia e ingeniería. Puedes ver una buena introducción a LaTeX en esta dirección (pdf): http://www.ctan.org/tex-archive/info/lshort/spanish.

Representación gráfica de funciones

Visto el ejemplo anterior, vemos que en Python es muy fácil representar gráficamente una función matemática. Para ello, debemos definir la función y luego generar un array con el intervalo de valores de la variable independiente que se quiere representar. Definamos algunas funciones trigonométricas y luego representémoslas gráficamente:

def f1(x):
    y = sin(x)
    return y

def f2(x):
    y = sin(x) + sin(5.0*x)
    return y


def f3(x):
    y = sin(x) * exp(-x/10.)
    return y

# array de valores a representar
x = linspace(0, 10*pi, 800)

p1, p2, p3 = plot(x, f1(x), x, f2(x), x, f3(x))

# Añado leyenda, tamaño de letra 10, en esquina superior derecha
legend(('Funcion 1', 'Funcion 2', 'Funcion 3'),
prop = {'size': 10}, loc='upper right')

xlabel('Tiempo / s')
ylabel('Amplitud / cm')
title('Representacion de tres funciones')

# Creo una figura (ventana), pero indico el tamaño (x,y) en pulgadas
figure(figsize=(12, 5))

show()

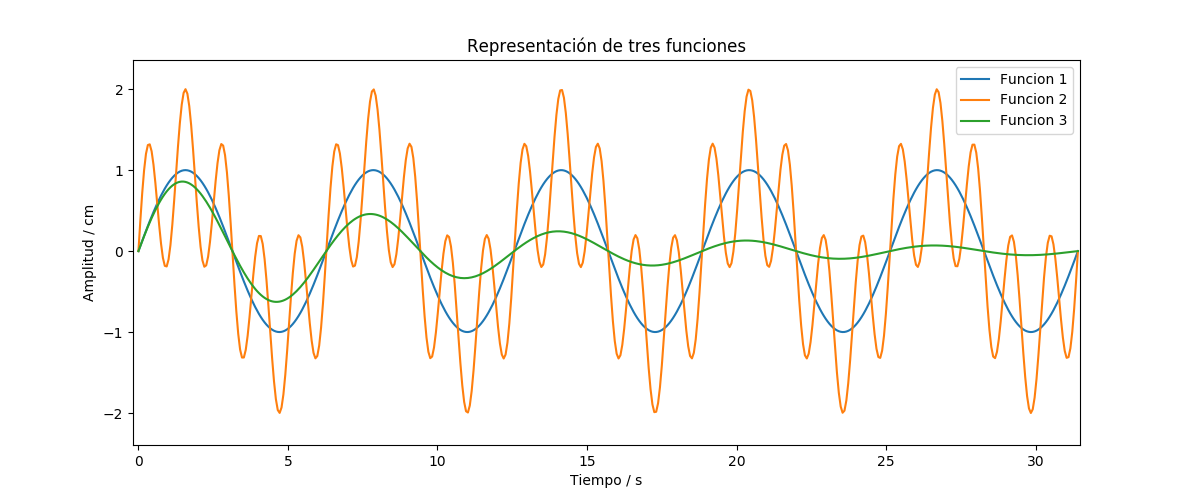
Nótese que hemos añadido una leyenda con la función legend() que admite como entrada una tupla con strings que corresponden consecutivamente a cada una de las curvas del gráfico. Alternativamente, se puede usar el parámetro label en cada plot() para identificar la gráfica y luego usar legend() sin parámetros, que usará la label indicada en cada gráfica como etiqueta.

# Plots con label
p1 = plot(x, f1(x), label='Funcion 1')
p2 = plot(x, f2(x), label='Funcion 2')
p3 = plot(x, f3(x), label='Funcion 3')

# Ahora se puede usar legend sin etiqueta, pero indico
# dónde quiero que se coloque
legend(loc='lower right')

Histogramas

Cuando tenemos un conjunto de datos numéricos, por ejemplo como consecuencia de la medida de una cierta magnitud y queremos representarlos gráficamente para ver la distribución subyacente de los mismos se suelen usar los gráficos llamados histogramas. Los histogramas representan el número de veces que los valores del conjunto caen dentro de un intervalo dado, frente a los diferentes intervalos en los que queramos dividir el conjunto de valores. En Python podemos hacer histogramas muy fácilmente con la función hist() indicando como parámetro un array con los números del conjunto. Si no se indica nada más, se generará un histograma con 10 intervalos (llamados bins, en inglés) en los que se divide la diferencia entre el máximo y el mínimo valor del conjunto. Veamos un ejemplo:

# Importamos el módulo de numeros aleatorios de numpy
from numpy import random

# utilizo la función randn() del modulo random para generar
# un array de números aleatorios con distribución normal
nums = random.randn(200)  # array con 200 números aleatorios

# generamos el histograma
h = hist(nums)
"""
(array([ 2, 10, 11, 28, 40, 49, 37, 12,  6,  5]),
array([-2.98768497, -2.41750815, -1.84733134, -1.27715452, -0.70697771,
    -0.13680089,  0.43337593,  1.00355274,  1.57372956,  2.14390637,
    2.71408319]),
<a list of 10 Patch objects>)
"""

Si no se le proporciona ningún otro argumento a randn() produce floats alrededor de 0 y con una varianza = 1.

Vemos que los números del array se dividieron automáticamente en 10 intervalos (o bins) y cada barra representa para cada una de ellos el número de valores que caen dentro. Si en lugar de usar sólo 10 divisiones queremos usar 20 por ejemplo, debemos indicarlo como un segundo parámetro:

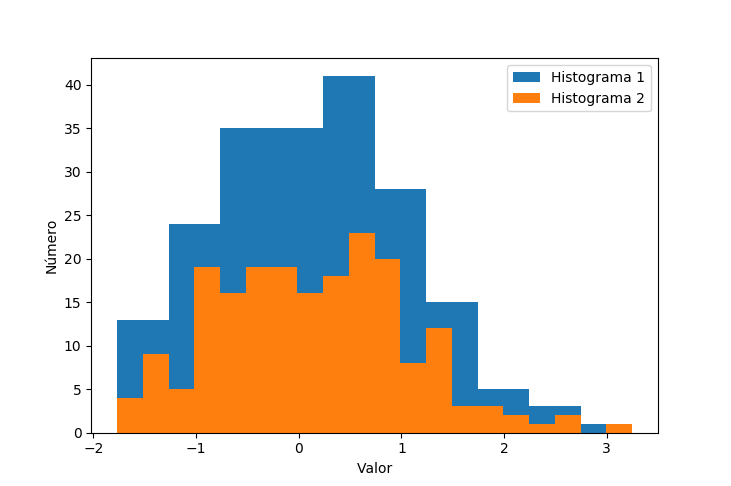
hist(nums, bins=20)

El la figura de abajo se muestra el resultado de superponer ambos histogramas. Nótese que la función hist() devuelve una tupla con tres elementos, que son un array con el número elementos en cada intervalo, un array con el punto del eje OX donde empieza cada intervalo y una lista con referencias a cada una de las barras para modificar sus propiedades (consulten el manual de matplotlib para encontrar más información y mayores posibilidades de uso).

Varias ventanas de gráficos

Se pueden hacer cuantas figuras independientes (en ventanas distintas) queramos con la función figure(n) donde n es el número de la figura. Cuando se crea una figura al hacer plot() se hace automáticamente figure(1), como aparece en el título de la ventana. Podríamos crear una nueva figura independiente escribiendo figure(2), en ese momento todos los comandos de aplican a figura activa, la figura 2. Podemos regresar a la primera escribiendo figure(1) para trabajar nuevamente en ella, por ejemplo:

p1, = plot(sin(x))       # Crea una figura en una ventana (Figure 1)

figure(2)                # Crea una nueva figura vacía en otra ventana (Figure 2)
p2, = plot(cos(x))       # Dibuja el gráfico en la figura 2
title('Funcion coseno')  # Añade un título a la figura 2

figure(1)                # Activo la figura 1
title('Funcion seno')    # Añade un título a la figura 2

Varios gráficos en una misma figura

En ocasiones nos interesa mostrar varios gráficos diferentes en una misma figura o ventana. Para ello podemos usar la función subplot(), indicando entre paréntesis un número con tres dígitos. El primer dígito indica el número de filas en los que se dividirá la figura, el segundo el número de columnas y el tercero se refiere al gráfico con el que estamos trabajando en ese momento. Por ejemplo, si quisiéramos representar las tres funciones anteriores usando tres gráficas en la misma figura, una al lado de la otra y por lo tanto con una fila y tres columnas, haríamos lo siguiente:

# Figura con una fila y tres columnas, activo primer subgráfico
subplot(131)
p1, = plot(x,f1(x),'r-')
# Etiqueta del eje Y, que es común para todas
ylabel('Amplitud / cm')
title('Funcion 1')

# Figura con una fila y tres columnas, activo segundo subgráfico
subplot(132)
p2, = plot(x,f2(x),'b-')
# Etiqueta del eje X, que es común para todas
xlabel('Tiempo / s')
title('Funcion 2')

# Figura con una fila y tres columnas, activo tercer subgráfico
subplot(133)
p3, = plot(x, f3(x),'g-')
title('Funcion 3')

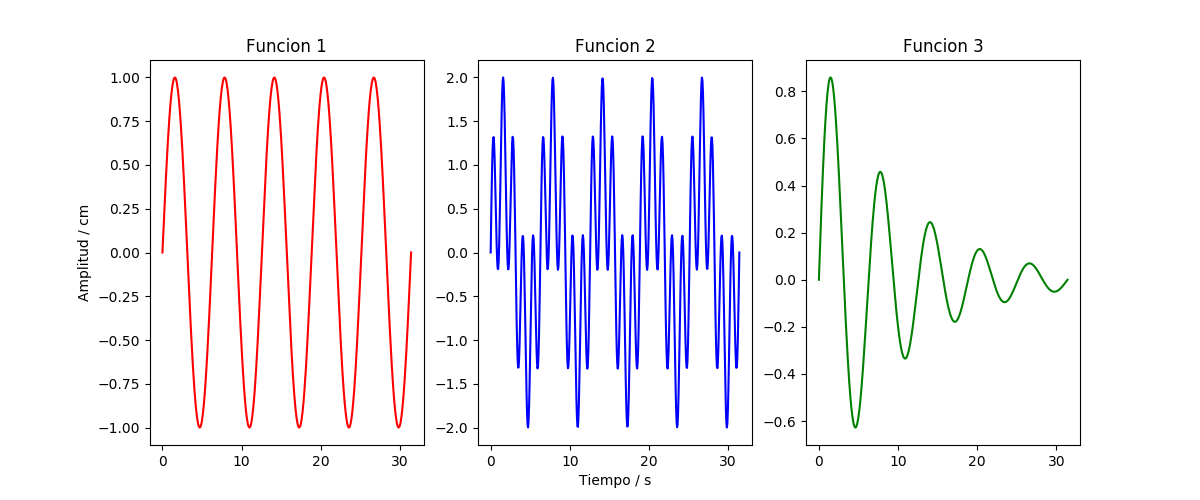
Al igual que con varias figuras, para dibujar en un gráfico hay que activarlo. De esta forma, si acabamos de dibujar el segundo gráfico escribiendo antes subplot(132) y queremos cambiar algo del primero, debemos activarlo con subplot(131) y en ese momento todas funciones de gráficas que hagamos se aplicarán a él.

Para crear gráficos que comparten ejes en una misma figura, podemos usar el submodulo <https://matplotlib.org/api/toolkits/axes_grid1.html> axes_grid1>__, que permite dividir la figura en varios gráficos del mismo o distinto tipo.

Datos experimentales con barras de error

Para representar barras error, matplotlib tiene una función específica alternativa a plot() llamada errorbar(), que funciona de forma similar pero no igual a plot(). La principal difirencia es que es obligatorio usar datos para x e y y como tercer parámetro se da el un float o array con el error en y, siendo opcional el error en x. Para dar el formato se debe usar el parámetro fmt="" como un string, que es igual al usado en plot().

Probemos a representar unos datos de medidas de desintegración radioactiva que tienen datos de error:

# El fichero tiene tres columnas separadas por ";"
# Tiempo en horas, masa en gramos y error de la medida de la masa
tiempo, masa, error = loadtxt("medidas_radio2.txt", delimiter=";", unpack=True)

# Doy un error fijo al eje x, que es opcional
xerror = 2.0

# Dibujo las medidas con errores, que pueden darse como un número
# fijo o un array, dibujando solo punto grandes ("o")
errorbar(tiempo, masa, yerr=error, xerr=xerror, fmt="o")

xlabel("Tiempo (horas)")
ylabel("Masa (gramos)")
savefig("grafica_desintegracion.png")

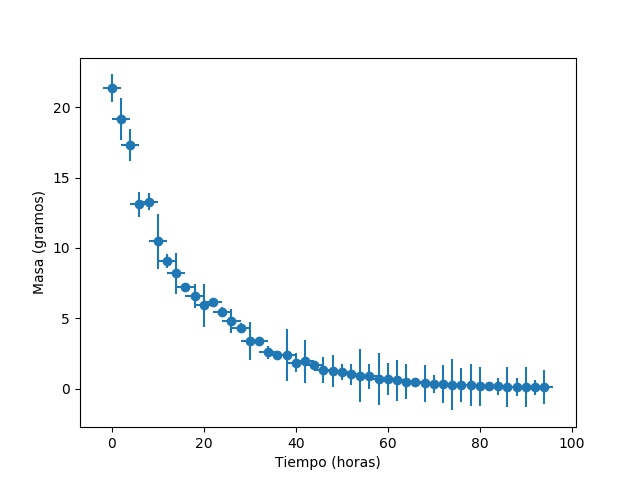
Podemos usar algunos elementos de dibujo para resaltar zonas del gráfico con línea o bandas horizontales y verticales. Las coordenadas se ponen siempre en coordenadas de la gráfica, pero se pueden poner límites opcionales que se indican como fracción del eje, siendo 0 el inicio del eje y 1 el final.

# Trazo una línea vertical en la coordenada x=10 color rojo (r)
# y con trazo punteado
axvline(10, color='r', ls="dotted")

# Línea horizontal en la coordenada y=10.4 color verde (g)
# que termina en la mitad de la gráfica (0.5, va de 0 a 1)
axhline(10.4, color='g', xmax=0.5)

# Banda horizontal de y=0 a y=2 de color azul (b)
# y 30% de transparencia (alpha=0.3)
axhspan(0, 2, alpha=0.3, color='b')

# Banda vertical de x=0 a x=4 de color amarillo
# y 30% de transparencia
axvspan(0, 4, alpha=0.3, color='y')

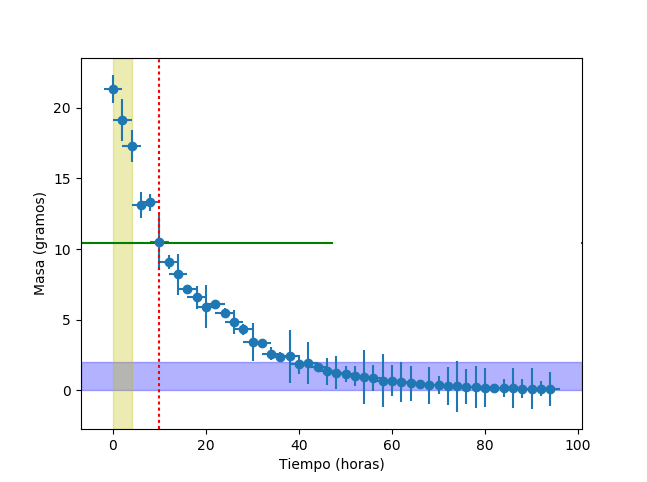
Fijémonos en el las marcas y etiquetas de los ejes, que se imprimieron automáticamente según los datos representados. Estos se pueden cambiar con las funciones xticks() y yticks(). Si se usan sin parámetros, simplemente nos devuelve una tupla de dos elementos: y array de índices de posición y una lista de etiquetas de texto. Pero si le datos como parámetro una tupla con posiciones y etiquetas será las que use para el dibujar el eje. En nuestra gráfica, el eje y va de 0 a 20 de cinco en cinco, pero supongamos que queremos poner más marcadores. Si le datos a yticks() un solo parametro de array, serán los valores que use como marcadores y etiquetas:

In[1]: yticks()  Marcadores y etiquetas de la gráfica acutual
Out[1]:
(array([  1.00000000e-03,   1.00000000e-02,   1.00000000e-01,
          1.00000000e+00,   1.00000000e+01,   1.00000000e+02,
          1.00000000e+03]), <a list of 7 Text yticklabel objects>)

In[2]: # Creo más marcardores en el eje Y, el indice y la etiqueta es la misma
In[3]: yticks(range(0,20,2))


In[5]: # Marcadores en un array de numeros y etiquetas en un array de strings
In[6]: marcadores = range(0, 30, 5)
In[7]: etiquetas = ["A", "B","C","D","E", "F"]
In[8]: yticks(marcadores, etiquetas)

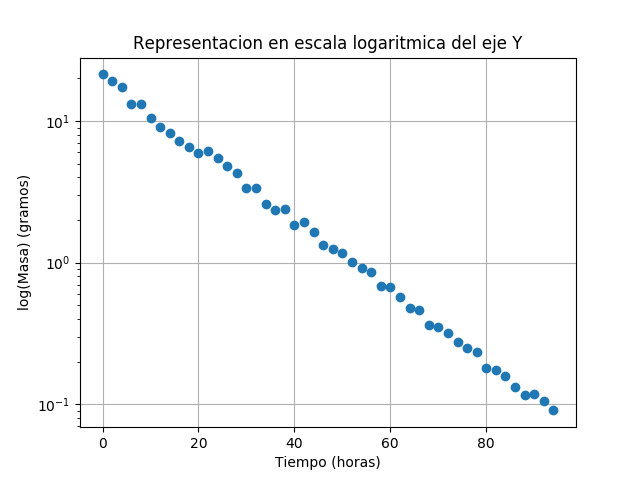
Hay veces que para algunos tipos de datos, conviene representar alguno de los ejes o ambos en escala logarítmica para apreciar mejor la evolución de la gráfica. Podemos usar las funciones semilogx(), semilogy() o loglog() para hacer un gráfico en escala logarítmica en el eje x, en el eje y o en ambos, respectivamente. Por ejemplo, para representar el gráfico anterior con el eje y en escala logarítmica, podemos hacer lo siguiente:

# Eje y en escala logarítmica
p1, = semilogy(d[0], d[1], 'o')

grid()
xlabel("Tiempo (horas)")
ylabel("log(Masa) (gramos)")
title('Representacion en escala logaritmica del eje Y')

Representación de datos bidimensionales

Los datos bidimensionales son valores de una magnitud física representada por una función que tiene dos variables independientes, normalmente x e y; se trata pues de representar funciones del tipo z=z(x,y), donde z puede representar flujo luminoso, presión atmosférica, altura del terreno, etc. Podemos usar la función imshow() para mostrar imágenes bidimensionales, que deben ser arrays 2D de numpy. La función imread() de matplotlib nos permite leer una imagen de bit en los formatos más comunes (jpg, png, svg), que lee datos multidimensionales a un array de tañano MxNxR, siendo M las filas, N las columnas y R la banda en caso de ser una imagen multicanal (a color RGB, por ejemplo).

# Leo la imagen png a array de numpy
img = imread("la_palma.png")
img = imread("datos/M31.jpg")

# imagen en color, tres bandas
imshow(img)

# Tomo la banda R
R = img[:, :, 0]
imshow(R, cmap=gray())


# Hacemos un zoom y escojemos la zona de interes
# xlim e ylim necesitan enteros
xlim0, xlim1 = array(xlim(), dtype=int)
ylim0, ylim1 = array(ylim(), dtype=int)

print(ylim0, ylim1)
# (328, 192)

# Hago una selección basada en los límites actuales de la grafica
# Atencion!: Hay que fijarse que Y es la primera dimension (primer eje) y por
# eso va de primero y ademas el origen está arriba a la izquierda, por lo
# hay que poner poner primero el segundo limite ylim1
seleccion = R[ylim1:ylim0, xlim0:xlim1]

# Quito los ejes
axis('off')

# Muestro la grafica con barra de color
imshow(seleccion, cmap=jet())
cb = colorbar()

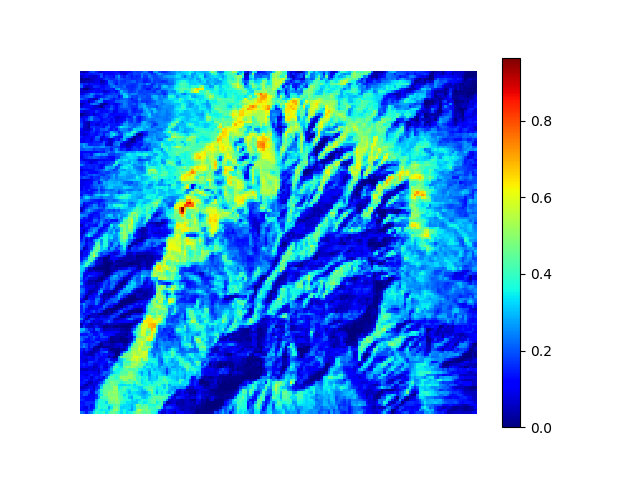
Sobre las imágenes 2D es posible crear contornos de niveles con contour(), dando los niveles como un array de números con los niveles deseados:

# Limpio la figura
clf()

# Muestro la imagen en gris y creo contornos
# con mapa de color jet()
imshow(seleccion, cmap=gray())
contour(seleccion, levels=arange(0,1,0.2), color=jet())

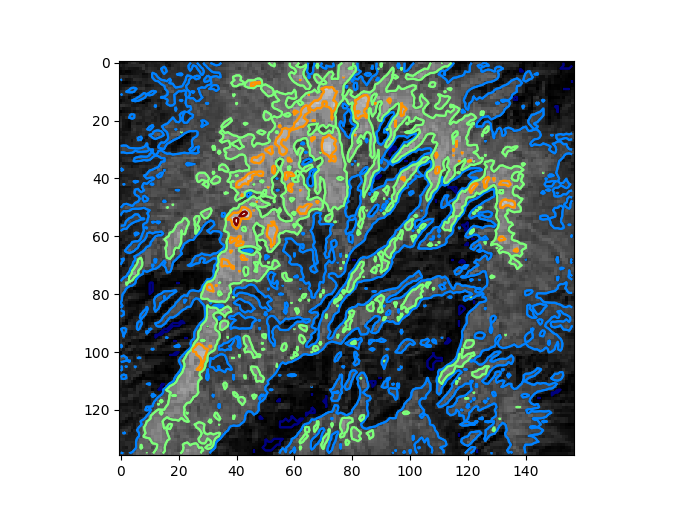
Guardando las figuras

Después de crear una figura con cualquiera de los procedimientos descritos hasta ahora podemos guardarla con la función savefig() poniendo como parámetro el nombre del fichero con su extensión. El formato de grabado se toma automáticamente de la extensión del nombre. Los formatos disponibles en Python son los más usuales: png, pdf, ps, eps y svg. Por ejemplo:

savefig("mi_grafica.eps")           # Guardo la figura en formato eps
savefig("mi_grafica.png", dpi=300)  # Guardo la figura en formato png a 300 DPI

Si el gráfico se va usar para imprimir, por ejemplo en una publicación científica o en un informe, es recomendable usar un formato vectorial como Postscript (ps) o Postscript encapsulado (eps), pero si es para mostrar por pantalla o en una web, el más adecuado es un formato de mapa de bits como png o jpg.

Gráficos 3D

Aunque matplotlib está especializado en gráficos 2D, incluye un toolkit para hacer gráficos 3D de muchos tipos usando OpenGL, que nos resolverá casi todas las necesidades para gráficos de este tipo.

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D, get_test_data
from matplotlib import cm

# Figura
fig = plt.figure()

# Tomo el eje actual y defino una proyección 3D
ax = gca(projection='3d')

# Dibujo 3D
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)

# el metodo meshgrid devuelve una matriz de coordenadas
# a partir de vectores de coordendas, que usamos para
# los datos del eje Z
X, Y = np.meshgrid(X, Y)

R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)

# Grafico surface en 3D
surface = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm, linewidth=0, antialiased=False)

# Límites del eje Z
ax.set_zlim(-1.01, 1.01)

# Barra de nivel, un poco más pequeña
fig.colorbar(surf, shrink=0.5, aspect=10)

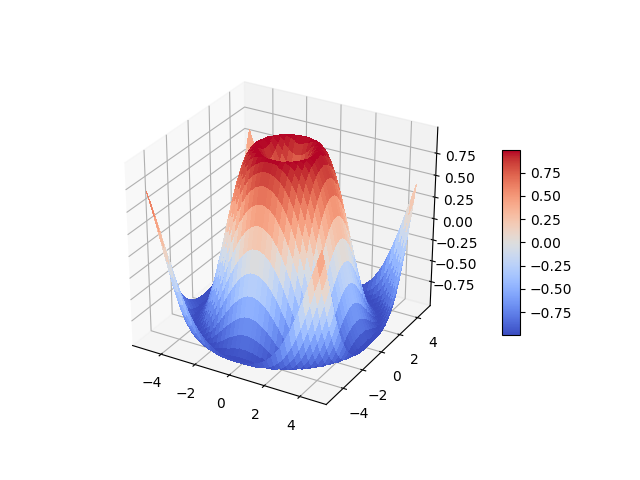
Si queremos hacer lo mismo con una imagen, debemos crear igualmente las matrices de coordenadas X e Y para cada pixel de la imagen. Podemos usar mgrid() que usa índices:

xx, yy = np.mgrid[0:seleccion.shape[0], 0:seleccion.shape[1]]

ax.plot_surface(xx, yy, seleccion ,rstride=1, cstride=1, cmap=plt.cm.gray, linewidth=0)

Mapas geográficos con Basemap

Se pueden crear mapas geográficos con matplotlib y representar datos sobre ellos usando la extensión (toolkit) basemap, que no viene por defecto con matplotlib por lo que hay que instalar previamente.

pip3 install basemap     # Instalación de Python estandar
conda install basemap    # Con Anaconda-Python

Para hacer un mapa hay que crear un instancia de mapa con coordenadas de centro, proyección, resolución y márgenes. Luego podemos crear un lista de coordenadas de latitud y longitud en grados y transformarlas a coordendas del mapa para poder representarla con cualquier función de pyplot(), generalmente plot() o scatter().

from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt

# Coordendas de Tenerife, en grados
lat, lon = 28.2419, -16.5937

# Mapa en alta resolución (h) con proyección mercator
map = Basemap(projection='merc', lat_0 = lat, lon_0 = lon,
    resolution = 'h', area_thresh = 0.1,
    llcrnrlon=lon-0.5, llcrnrlat=lat-0.5,
    urcrnrlon=lon+0.5, urcrnrlat=lat+0.5)

# Líneas de costas y paises, aunque en este ejemplo no se ven
map.drawcoastlines()
map.drawcountries()

map.fillcontinents(color = '#cc9966')
map.drawmapboundary()

# Coordenadas para dibujar en el map
lats = [28.5068, 28.2617, 28.3310]
lons = [-16.2531, -16.5526, -16.8353]

x,y = map(lons, lats)
map.plot(x, y, '*r', markersize=6)

plt.show()

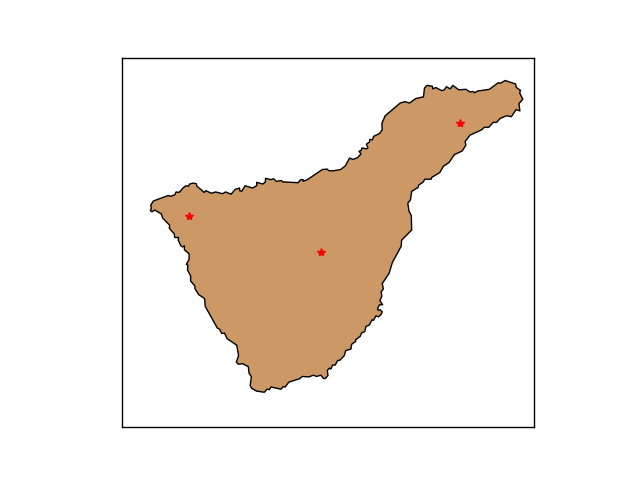
Nota

En el caso concreto de gráficos para Astronomía, el módulo APLpy genera gráficos para imágenes FITS que permite usar la astrometría de las cabeceras y crear ejes con coordenadas astronómicas, entre otras cosas.

Ejercicios

1. La curva plana llamada trocoide, una generalización de la cicloide, es la curva descrita por un punto P situado a una distancia b del centro de una circunferencia de radio a, a medida que rueda (sin deslizar) por una superficie horizontal. Tiene por coordenadas (x,y) las siguientes:

   \[x = a \ \phi - b \ sen \phi \ \ \ ,\ \ \ y = a - b\ cos \phi\]

   Escribir un programa que dibuje tres curvas (contínuas y sin símbolos), en el mismo gráfico cartesiano (OX,OY), para un intervalo \(\phi=[0.0,18.0]\) (en radianes) y para los valores de a=5.0 y b=2.0, 5.0 y 8.0 . Rotular apropiadamente los ejes e incluir una leyenda con los tres valores de que distinguen las tres curvas.

2. Dibujar las diferentes trayectorias de los proyectiles disparados por un cañón situado en un terreno horizontal para diferentes ángulos de elevación (inclinación respecto de la horizontal) en un intervalo de tiempo de 0 a 60 s. El cañón proporciona una velocidad inicial de 300 m/s. Dibujarlas para los ángulos de elevación siguientes: 20, 30, 40, 50, 60 y 70 grados y suponer que el cañón está situado en el origen de coordenadas. Rotular apropiadamente los ejes e insertar una leyenda que identifique las diferentes trayectorias. Recordar que el proyectil no puede penetrar en el suelo de forma que hay que establecer los límites apropiados para el dibujo.

3. Con la serie de Gregory-Leibnitz para el cálculo de \(\pi\) usada anteriormente en el problema 5.5:

   \[4 \sum^n_{k=1} \frac{(-1)^{k+1}}{2k - 1}\]

   el valor obtenido de \(\pi\) se acerca lentamenta al verdadero con cada término que se añada. Calculen todos los valores que va tomando \(\pi\) con cada término añadido y representar en una figura con dos gráficas (usando subplot()) los primeros 300 valores que toma \(\pi\) frente al número de términos usados en una de ellas y el valor absoluto de la diferencia entre el valor calculado y el real frente al número de elementos en la otra.

4. El movimiento de un oscilador amortiguado se puede expresar de la siguiente manera:

   \[x = A_0 e^{-k\omega t} \cos{(\omega t + \delta)}\]

   Siendo \(A_0\) la amplitud inicial, \(\omega\) la fecuencia angular de oscilación y k el factor de amortiguamiento. Representar gráficamente el movimiento de un oscilador amortiguado de amplitud inicial de 10 cm y frecuencia de 10 ciclos/s y \(\delta=\pi/8\) con factores de amortiguamiento de 0.1, 0.4, 0.9 y 1.1 durante 10 s. Incluya una leyenda identificativa de las curvas dibujadas.

   Para el gráfico correspondiente a k=0.1 unir con líneas a trazos los valores máximos por un lado y los valores mínimos por otro del movimiento oscilatorio. Nótese que corresponden a las curvas para las que \(x=A_0 e^{-k\omega t}\) y \(x=-A_0e^{-k\omega t}\).