La librería científica Scipy¶
Scipy es el paquete científico (es decir, un módulo que tiene otros módulos) más completo, que incluye interfases a librerías científicas muy conocidas como LAPACK, BLAS u ODR entre muchas otras . Si importamos scipy para tener su espacio de nombres y consultamos la ayuda, vemos todos los módulos que posee:
In [1]: import scipy
In [2]: help(scipy)
cluster --- Vector Quantization / Kmeans
fftpack --- Discrete Fourier Transform algorithms
integrate --- Integration routines
interpolate --- Interpolation Tools
io --- Data input and output
lib --- Python wrappers to external libraries
lib.lapack --- Wrappers to LAPACK library
linalg --- Linear algebra routines
misc --- Various utilities that don't have
another home.
ndimage --- n-dimensional image package
odr --- Orthogonal Distance Regression
optimize --- Optimization Tools
signal --- Signal Processing Tools
sparse --- Sparse Matrices
sparse.linalg --- Sparse Linear Algebra
sparse.linalg.dsolve --- Linear Solvers
sparse.linalg.dsolve.umfpack --- :Interface to the UMFPACK library:
Conjugate Gradient Method (LOBPCG)
sparse.linalg.eigen.lobpcg --- Locally Optimal Block Preconditioned
Conjugate Gradient Method (LOBPCG) [*]
special --- Airy Functions [*]
lib.blas --- Wrappers to BLAS library [*]
sparse.linalg.eigen --- Sparse Eigenvalue Solvers [*]
stats --- Statistical Functions [*]
lib --- Python wrappers to external libraries
[*]
lib.lapack --- Wrappers to LAPACK library [*]
integrate --- Integration routines [*]
ndimage --- n-dimensional image package [*]
linalg --- Linear algebra routines [*]
spatial --- Spatial data structures and algorithms
special --- Airy Functions
stats --- Statistical Functions
Ajustes lineales y no lineales¶
Si simplemente necesitamos hacer ajustes básicos de polinomios, lo podemos hacer fácilmente sólo con numpy:
# Librería numpy
import numpy as np
# Datos experimentales
x = np.array([ 0., 1., 2., 3., 4.])
y = np.array([ 10.2 , 12.1, 15.5 , 18.3, 20.6 ])
# Ajuste a una recta (polinomio de grado 1)
p = np.polyfit(x, y, 1)
print(p)
# imprime [ 2.7 9.94]
en este ejemplo np.polyfit() devuelve la lista de parámetros p de la recta, por lo que el modelo lineal \(f(x) = ax + b\) de nuestros datos será:
\(y(x) = p_0 x + p_1 = 2.7x + 9.94\)
Ahora podemos dibujar los datos experimentales y la recta ajustada:
from matplotlib import pyplot as plt
# Valores de y calculados del ajuste
y_ajuste = p[0]*x + p[1]
# Dibujamos los datos experimentales
p_datos, = plt.plot(x, y, 'b.')
# Dibujamos la recta de ajuste
p_ajuste, = plt.plot(x, y_ajuste, 'r-')
plt.title('Ajuste lineal por minimos cuadrados')
plt.xlabel('Eje X')
plt.ylabel('Eje Y')
plt.legend(('Datos experimentales', 'Ajuste lineal'), loc="upper left")
plt.show()
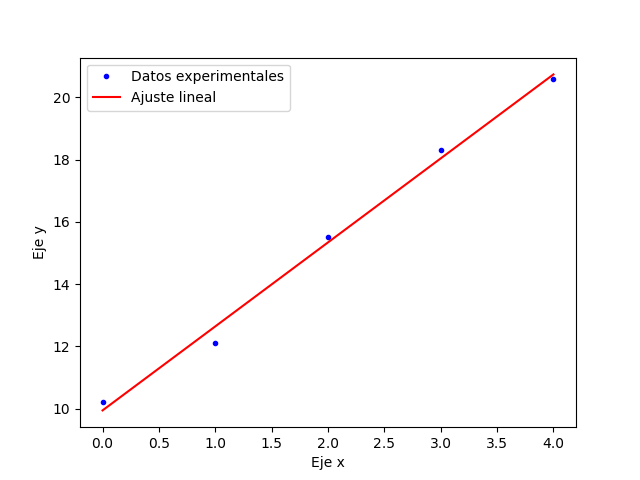
Como se ve en este ejemplo, la salida por defecto de np.polyfit() es un array con los parámetros del ajuste. Sin embargo, si se pide una salida detalla con el parámetro full=True (por defecto full=False), el resultado es una tupla con el array de parámetros, el residuo, el rango, los valores singulares y la condición relativa. Nos interesa especialmente el residuo del ajuste, que es la suma cuadrática de todos los resíduos \(\sum^n_{i=1} \lvert y_i - f(x_i)\rvert^2\). Para el ejemplo anterior tendríamos lo siguiente:
# Ajuste a una recta, con salida completa
resultado = np.polyfit(x, y, 1, full=True)
print(resultado)
""" Imprime tupla
(array([ 2.7 , 9.94]), # Parámetros del ajuste
array([ 0.472]), # Suma de residuos
2, # Rango de la matriz del sistema
array([ 2.52697826, 0.69955764]), # Valores singulares
1.1102230246251565e-15) # rcond
"""
Ajuste de funciones generales¶
Si queremos hacer un ajuste general, no necesariamente polinómico, debemos usar alguno de los métodos del paquete optimize, que contiene varios optimizadores locales y globales. El más común es leastsq que, al ser un optimizador, hay que definir previamente una función residuo que es la que realmente se va minimizar.
import numpy as np
from matplotlib import pyplot as plt
from scipy.optimize import leastsq
# Datos de laboratorio
datos_y = np.array([ 2.9, 6.1, 10.9, 12.8, 19.2])
datos_x = np.array([ 1.0, 2.0, 3.0, 4.0, 5.0])
# Función para calcular los residuos, donde
# se calcula (datos - modelo)
def residuos(p, y, x):
error = y - (p[0]*x + p[1])
return error
# Parámetros iniciales estimados
# y = p0[0]*x + p0[0]
p0 = [2.0, 0.0]
# Hacemos el ajuste por minimos cuadrados con leastsq(). El primer parámetro
# es la funcion de residuos, luego los parámetro iniciales y una tupla con los
# argumentos de la funcion de residuos, en este caso, datos_y y datos_x en
# ese orden, porque así se definió la función de error
ajuste = leastsq(residuos, p0, args=(datos_y, datos_x))
# El resultado es una lista, cuyo primer elemento es otra
# lista con los parámetros del ajuste
print(ajuste[0])
# array([ 3.93, -1.41])
Veamos otro ejemplo para ajustar una función seno:
import numpy as np
from matplotlib import pyplot as plt
from scipy.optimize import leastsq
from scipy import random
# Generamos unos datos artificiales para hacer el ejemplo
# A datos_y se le añade "ruido" que simula error de
# medida, añadiendole un valor aleatorio
datos_x = np.arange(0, 0.1, 0.005)
A, k, theta = 10.0, 33.3, np.pi/5.0
y_real = A*np.sin(2*np.pi*k*datos_x + theta)
datos_y = y_real + 2*random.randn(len(datos_x))
# Ahora se trata de ajustar estos datos una función
# modelo tipo senoidal A*sin(2*pi*k*x + theta)
# Defino la funcion de residuos
def residuos(p, y, x):
A, k, theta = p
error = np.abs(y - A*np.sin(2*np.pi*k*x + theta))
return error
# Parámetros iniciales
p0 = [8.0, 40.0, np.pi/3]
# hacemos el ajuste por minimos cuadrados
ajuste = leastsq(residuos, p0, args=(datos_y, datos_x))
# El resultado es una lista, cuyo primer elemento es otra
# lista con los parámetros del ajuste.
print(ajuste[0])
# Ahora muestro los datos y el ajuste gráficamente
plt.plot(datos_x, datos_y, 'o') # datos
# Defino la funcion modelo, para representarla gráficamente
def funcion(x, p):
return p[0]*np.sin(2*np.pi*p[1]*x + p[2])
# genero datos a partir del modelo para representarlo
x1 = np.arange(0, datos_x.max(), 0.001) # array con muchos puntos de x
y1 = funcion(x1, ajuste[0]) # valor de la funcion modelo en los x
plt.plot(x1, y1, 'r-')
plt.xlabel('Eje X')
plt.ylabel('Eje Y')
plt.title('Ajuste de funcion seno con leastsq')
plt.legend(('Datos', 'Ajuste lineal'))
plt.show()
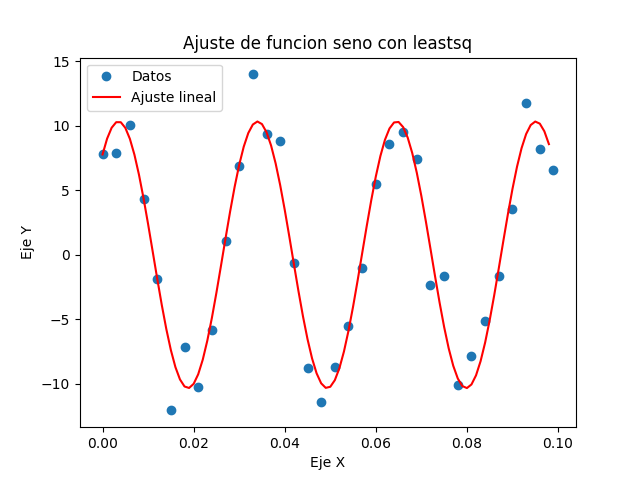
Este ejemplo es bastante alaborado porque hemos usado un optimizador general para hacer un ajuste, pero podemos usar curve_fit() para ahorrarnos la función residuo.
La anterior es una manera artesanal de hacer el ajuste, al construir la función de error. Para un ajuste de datos
from scipy.optimize import curve_fit
curve_fit(funcion, datos_x, datos_y, p0)
(array([ -9.787095 , 32.91201348, -2.3390355 ]),
array([[ 0.20148401, -0.00715614, 0.00215931],
[-0.00715614, 0.07184634, -0.02241144],
[ 0.00215931, -0.02241144, 0.00925902]]))
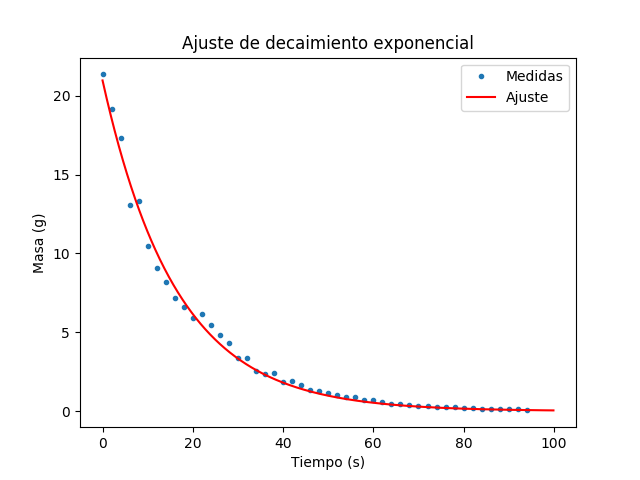
Vamo a probar esto con una ley de decaimiento exponencial:
# Cargo los datos experimentales a un array
# Los datos están delimitados por ";" y uso unpack
# para que ponga primero las columas y pueda desenpaquetarlas
# en variables
tiempo, masa, error = np.loadtxt("medidas_radio.txt", delimiter=";", unpack=True)
# Compruebo como ser ven los datos
plot(tiempo, masa, '.')
def decaimiento(x, a, b):
"""Ley de decaimiento exponencial"""
return a * exp(-b*x)
# Ajuste de los datos
# curve_fit devuelve dos variables, los parámetros del ajuste y
# la matriz de covarianza
popt, pcov = curve_fit(decaimiento, tiempo, masa)
# Ahora creo una curva teórica a partir del modelo ajustado
times = np.arange(0, 100, 0.1)
model = decaimiento(times, *popt)
plt.plot(times, model, '-r')
plt.legend(('Medidas', 'Ajuste'))
plt.xlabel("Tiempo (s)")
plt.ylabel("Masa (g)")
plt.title("Ajuste de decaimiento exponencial")
# Guardo la grafica
plt.savefig("ajuste.png")
# Para mostrar la gráfica por pantalla
plt.show()
Interpolación de datos¶
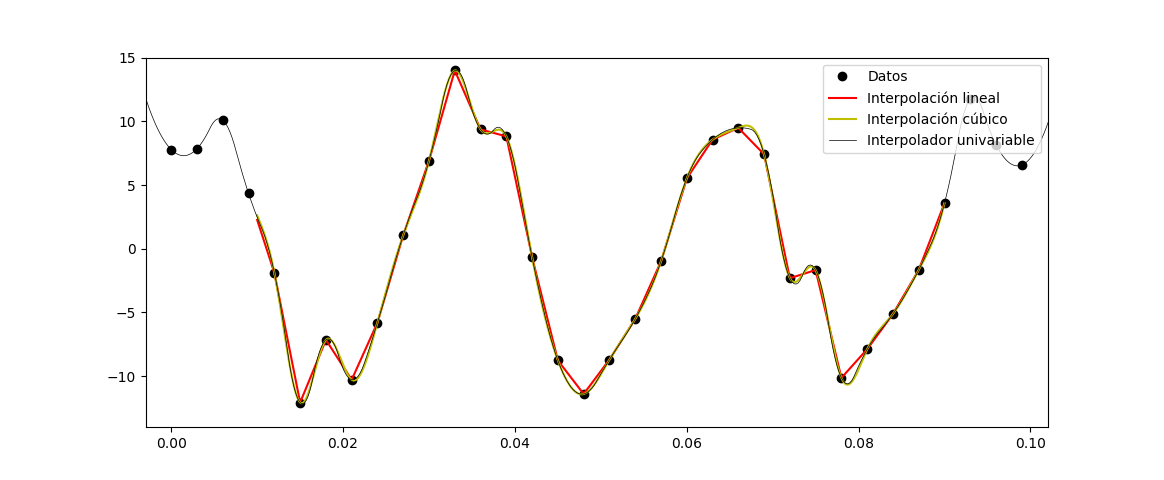
El módulo interpolate contiene rutinas de interpolación basadas en la conocida librería FITPACK en Fortran; resulta muy útil en partes de datos donde no hay suficientes medidas. Los interpoladores funcionan creando una función interpoladora de orden predefinido, usando los datos de medidas. Luego se aplica esta función de interpolación a un array de datos más denso que la muestre. Consideremos los datos senoidales que vimos antes:
from scipy.interpolate import interp1d
interpolador_lineal = interp1d(datos_x, datos_y)
interpolador_cubico = interp1d(datos_x, datos_y, kind='cubic')
x_inter = linspace(0.01, 0.09, 500)
y_inter_l = interpolador_lineal(x_inter)
y_inter_c = interpolador_cubico(x_inter)
plt.plot(datos_x, datos_y, 'ok', label="Datos")
plt.plot(x_inter, y_inter_l, 'r', label="Interpolación lineal")
plt.plot(x_inter, y_inter_c, 'y', label="Interpolación cúbico")
# Si usamos InterpolatedUnivariateSpline podemos interpolar fuera
# del rango de los datos
from scipy.interpolate import InterpolatedUnivariateSpline
# Array de valores más denso que los datos originales, pero
# dentro del rango de los datos
x_inter = np.linspace(-0.01, 0.11, 500)
interpolador = InterpolatedUnivariateSpline(datos_x, datos_y, k=2)
y_inter_u = interpolador(x_inter)
plot(x_inter, y_inter_u, 'k', lw=0.5, label="Interpolador univariable")
xlim(-0.003, 0.102)
ylim(-14, 15)
legend()
Aunque este es el método más usado para interpolar, tiene el problema que no permite interpolar puntos fuera del rango de las medidas. Esto se puede resolver con la función InterpolatedUnivariateSpline()
Integración numérica¶
Intentemos integrar numéricamente la integral:
\(\int_{-2}^{2} 2*\exp(\frac{-x^2}{5}) ~dx\)
def func1(x):
return 2.0*exp(-x**2/5.0)
# integración entre -2 y +2
int1, err1 = integrate.quad(func1, -2, +2)
print(int1,err1)
(6.294530963693763, 6.9883332051087914e-14)
Si ahora hacemos la misma integral pero desde \(-\infty\) hasta \(+\infty\) obtendremos toda el área bajo la curva definida en el integrando:
# integración entre -infinito y +infinito
In [10]: int2, err2 = integrate.quad(func1, -Inf, +Inf)
# y el resultado obtenido es:
In [11]: print(int1, err1)
(7.9266545952120211, 7.5246691415403668e-09)
Manipulación de arrays 2D: imágenes¶
El módulo ndimage ofrece manipulación y filtrado básicos de imágenes, dados como array de numpy.
In [20]: from scipy import misc
In [21]: from scipy import ndimage as nd
In [22]: img = misc.face(gray=True)
In [23]: shifted_img = nd.shift(img, (50, 50))
In [24]: shifted_img2 = nd.shift(img, (50, 50), mode='nearest')
In [25]: rotated_img = nd.rotate(img, 30)
In [26]: cropped_img = img[50:-50, 50:-50]
In [27]: zoomed_img = nd.zoom(img, 2) # Interpola la imagen
In [28]: zoomed_img.shape
# (1536, 2048)
In [30]: noisy_img = np.copy(img).astype(np.float)
In [31]: noisy_img += img.std()*0.5*np.random.standard_normal(img.shape)
In [32]: blurred_img = nd.gaussian_filter(noisy_img, sigma=3)
In [33]: median_img = nd.median_filter(blurred_img, size=5)
In [34]: from scipy import signal
In [35]: wiener_img = signal.wiener(blurred_img, (5,5))
In [40]: plt.subplot(221)
In [41]: plt.imshow(img)
In [42]: plt.subplot(222)
In [43]: plt.imshow(blurred_img)
In [44]: plt.subplot(223)
In [45]: plt.imshow(median_img)
In [46]: plt.subplot(224)
In [47]: plt.imshow(wiener_img)

Para más utilidades de manipulación de imágenes más sofisticadas conviene usar http://scikit-image.org o http://opencv.org
Módulo de constantes físicas¶
Scipy contiene un práctico módulo de constantes físicas.
In [1]: from scipy import constants as C
In [2]: C.c # Velocidad de la luz en m/s
Out[2]: 299792458.0
In [4]: C.e # Carga del electrón
Out[4]: 1.602176565e-19
In [6]: C.atmosphere
Out[7]: 101325.0
In [7]: C.mmHg
Out[7]: 133.32236842105263
In [8]: C.Julian_year
Out[8]: 31557600.0
In [9]: C.Avogadro
Out[9]: 6.02214129e+23
In [10]: C.parsec
Out[10]: 3.0856775813057292e+16
In [11]: C.Stefan_Boltzmann
Out[11]: 5.670373e-08
In [13]: C.convert_temperature(np.array([0, 100.0]), 'Celsius', 'Kelvin') # Conversor temps
Out[13]: array([ 273.15, 373.15])
In [14]: C.day # Dia en segundos
Out[14]: 86400.0
In [15]: C.pico # Prefijos del SI
Out[15]: 1e-12
In [16]: C.oz
Out[16]: 0.028349523124999998
In [17]: # Constantes físicas de CODATA 2014
In [18]: C.find('atm')
Out[18]: ['standard atmosphere']
In [19]: C.physical_constants['standard atmosphere']
Out[19]: (101325.0, 'Pa', 0.0)
Ejercicios¶
El fichero de texto medidas_PV_He.txt posee medidas de presión y volumen para 0.1 mol de helio, que se comprime sistemáticamente a temperatura constante. Este experimento se realiza a tres temperaturas distintas. Suponiendo que el gas se comporta idealmente y por tanto que se verifica que PV=nRT, representar los datos y realizar un ajuste lineal P(V) para cada temperatura. ¿Cuánto vale la constante de gases ideales según el experimento?
Para una muestra que contiene 10g de yodo 131 (semivida de 8 días), se hacen diariamente cinco medidas independientes a lo largo de 60 días. Esas medidas están en el fichero medidas_decaimiento_yodo131b.txt, donde cada fila corresponde a cada una de las 5 medidas realizadas diariamente en gramos de yodo que queda. Representar en un gráfico con puntos las cinco medidas con colores distintos para cada una y ajustar a cada una la curva teórica de decaimiento. Imprimir por pantalla los parámetros de cada uno de los cinco ajustes.
Hacer una función que cree una máscara circular (todos los valores son cero, excepto una zona circular de radio
Ry centrada en un punto arbitrario) con un array 2D para la imagen del castor usada anteriormenteface = misc.face(gray=True).